Could Mortgages be Cheaper than Cash?
John Chavez
June 21, 2020

Intro
If you bought a house with a mortgage, and put all of your unused money in the stock market, could you end up with more money than if you’d bought the house with cash?
The answer might surprise you.
Scenario
Let’s assume:
- You purchased a $2M home with a 20% ($400K) downpayment on January 1, 1989. (We choose ’89 so we can backtest a 30 year mortgage through 2019.)
- You invested whatever unspent money you had in the S&P 500.
- Every month, you withdrew the exact mortgage payment from your investment holdings.
- Your interest rate is 10%. (The 1989 average was 10.32%.)
- You locked in your interest rate in 1989 and never refinanced your mortgage.
To test this strategy, we need to know (a) how the stock market performed over the 30-year mortgage period (b) how much our mortgage would’ve cost.
The Market
Let’s take a quick look at how the S&P 500 performed between 1989 and 2019.
# Data from Yahoo Finance
"https://query1.finance.yahoo.com/v7/finance/download/%5EGSPC?period1=599616000&period2=1577836800&interval=1mo&events=history" %>%
read.csv() %>%
mutate(Date = as.POSIXct(Date)) %>%
subset(Date>='1989-01-01') %>%
select(Date, Close) %>%
rename(Price=Close) -> sp500
sp500 %$%
xts(Price, Date) %>%
dygraph() %>%
dySeries("V1","S&P 500 Price")Between 1989 and 2019, the value of the S&P 500 exploded 986%.
sp500 %$% first(Price) -> start
sp500 %$% last(Price) -> end
((end-start)/start * 100) %>% round(2) %>% paste(.,"%") %>% print()## [1] "986.09 %"If you could almost 10x your money, would you be able to undo the hemmorhaging cost of paying off a mortgage?
The Mortgage
In order to calculate how much your mortgage payment would be each month, you need to know your p (principal), r (interest rate), and n (number of payments). Once you have those, you can plug them into this well-known formula:
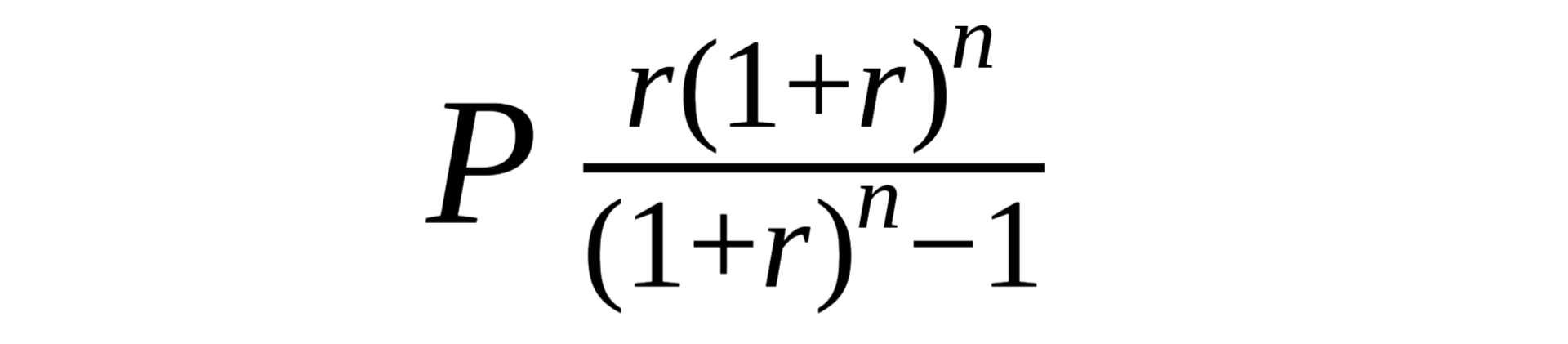
Let’s look at our scenario’s mortgage payments:
monthly_payment <- function(p,r,n){
p * (((r*(1+r)^n) / (((1+r)^n)-1)))
}
p <- 1600000 # principal
r <- .10/12 # monthly interest rate
n <- 30*12 # number of lifetime payments
monthly_payment(p,r,n) %>% round(2) %>% paste("$",.) %>% print()## [1] "$ 14041.15"Every month you’ll get a bill from the bank for $14,041.15. What will the overall cost of the mortgage be? The monthly payment * the number of months you pay it.
(monthly_payment(p,r,n)*30*12) %>% round(2) %>% paste("$",.) %>% print()## [1] "$ 5054812.24"The total amount of money you’ll have to give the bank for this $2M house will be over $5M. Herein lies the essential problem: mortgages are incredibly expensive.
Still, are the stock market’s gains enough to overcome the cost of the mortgage?
Historical
Historically, no. The total amount of money you’ll end up losing, even with the sizable monthly increases in the S&P 500, is $3.83M. This is opposed to the $2M loss you’d incur if you’d simply bought the house with cash outright.
sp500 %<>%
mutate(
p = ifelse(!is.na(lag(Price)), 1 + ((Price - lag(Price)) / Price), 1),
Outright=-2000000)
run_sim <- function(df, r){
m <- monthly_payment(1600000, r/12, 30*12)
df %>% mutate(Mortgage = Reduce(f = function(prev, i) (prev) * p[i] - m, x = seq_along(Date), init = 1600000, acc = TRUE)[-1]) %>% select(Mortgage)
}
run_sim(sp500, .10) %>%
cbind(sp500) %>%
select(Date, Mortgage, Outright) %>%
read.zoo() %>%
dygraph() %>%
dyOptions(maxNumberWidth = 10)Theoretical
We know that historically, if you had a (then normal) 10% interest rate, this strategy would’ve failed. But does it always fail? Would the answer have been different if you got a better interest rate on your mortgage?
We can run our simulation with 10 different interest rates:
rates <- c(.05, .06, .07, .075, .08, .085, .09, .10, .11, .12)
rate_names <- map_chr(rates, function(x) paste(as.character(x*100),"%",sep=""))
run_sim(sp500, rates) -> x
do.call(rbind, x$Mortgage) -> x
cbind(sp500, x) -> x
rate_names -> colnames(x)[5:14]
x %>%
select(-Price, -p) %>%
read.zoo() %>%
dygraph() %>%
dyOptions(maxNumberWidth = 10)If you got a mortgage with an interest rate below 8.5% in 1989, you would’ve saved money as compared to buying the house with cash. Slight changes in the mortgage interest rate can make a huge impact on the overall cost of the mortgage rate, as 30-year mortgages are compounded 360 times over their lifetime.
Conclusion
If you expect the stock market to continue on as it did in the past 30 years – a couple major recessions, but overall positive growth – then you might want to consider this mortgage+stocks strategy. If you can lock in a low interest rate, you might be able to make up for your mortgage’s cost just by holding the S&P.

